Geodesic distance transform in python
%pylab inline
from scipy.ndimage.morphology import distance_transform_edtBelow, I used the Euclidean distance transform implemented in python. This function doesn’t take into account the topology of the surface represented by the mask
l = 100
x, y = np.indices((l, l))
center1 = (50, 20)
center2 = (28, 24)
center3 = (30, 50)
center4 = (60,48)
radius1, radius2, radius3, radius4 = 15, 12, 19, 12
circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
# 3 circles
img = circle1 + circle2 + circle3 + circle4
mask = ~img.astype(bool)
img = img.astype(float)
m = ones_like(img)
m[center1] = 0
#imshow(distance_transform_edt(m), interpolation='nearest')
m = ma.masked_array(distance_transform_edt(m), mask)
imshow(m, interpolation='nearest')
I implemented the Dijkstra algorithm to apply a geodesic distance transform to the shape above:
def geodesic_distance_transform(m):
mask = m.mask
visit_mask = mask.copy() # mask visited cells
m = m.filled(numpy.inf)
m[m!=0] = numpy.inf
distance_increments = numpy.asarray([sqrt(2), 1., sqrt(2), 1., 1., sqrt(2), 1., sqrt(2)])
connectivity = [(i,j) for i in [-1, 0, 1] for j in [-1, 0, 1] if (not (i == j == 0))]
cc = unravel_index(m.argmin(), m.shape) # current_cell
while (~visit_mask).sum() > 0:
neighbors = [tuple(e) for e in asarray(cc) - connectivity
if not visit_mask[tuple(e)]]
tentative_distance = [distance_increments[i] for i,e in enumerate(asarray(cc) - connectivity)
if not visit_mask[tuple(e)]]
for i,e in enumerate(neighbors):
d = tentative_distance[i] + m[cc]
if d < m[e]:
m[e] = d
visit_mask[cc] = True
m_mask = ma.masked_array(m, visit_mask)
cc = unravel_index(m_mask.argmin(), m.shape)
return mgdt = geodesic_distance_transform(m)imshow(gdt, interpolation='nearest')
colorbar()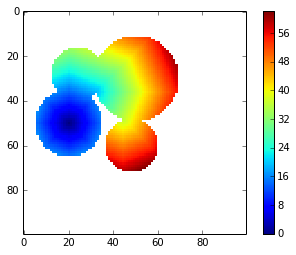
If someone have a faster implementation in python, I’m interested in! You can contribute to the code by giving an answer on stackoverflow.
If you want to ask me a question or leave me a message add @bougui505 in your comment.